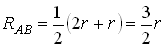ЛАБОРАТОРНЫЕ РАБОТЫ

Исследование сложных цепей постоянного электрического тока

Цель: изучить приемы расчета сложных электрических цепей постоянного тока.

1. Краткое теоретическое описание.

Сложные цепи не всегда удается представить в виде блоков последовательно и параллельно соединенных сопротивлений. Как же находить сопротивление таких цепей? Иногда эту задачу можно существенно упростить, если схема обладает симметрией.

Рис.1.

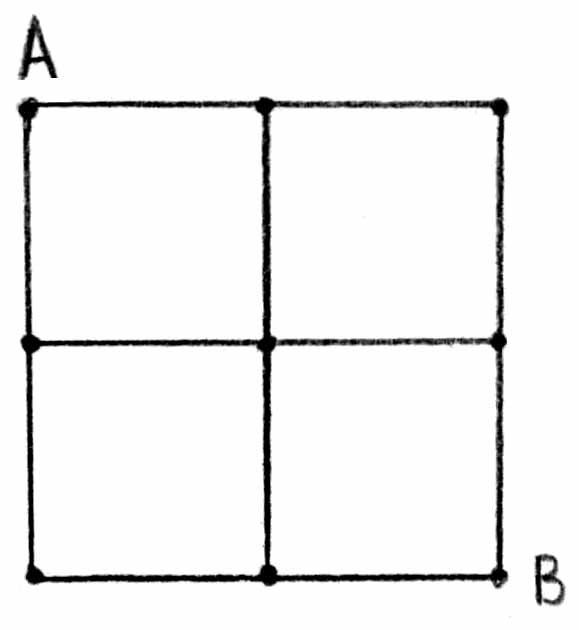
Рассмотрим в качестве примера такой цепи участок металлической сетки с одинаковыми сопротивлениями r:

Каково сопротивление между точками А и В?

Представить эту цепь в виде блоков последовательно и параллельно соединенных сопротивлений не удается. Как же быть?

Рис.2.

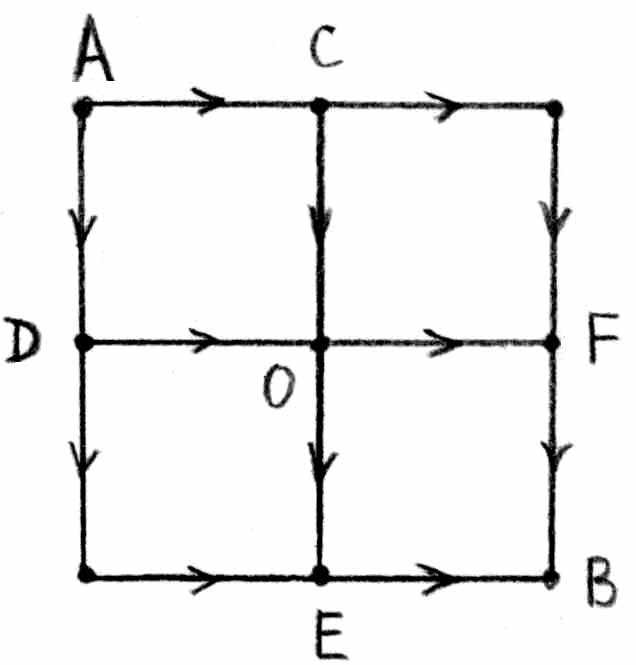
Пусть к точкам А и В подключен источник тока.

Посмотрим на токи, которые будут течь через элементы металлической сетки.

 Рис.3.

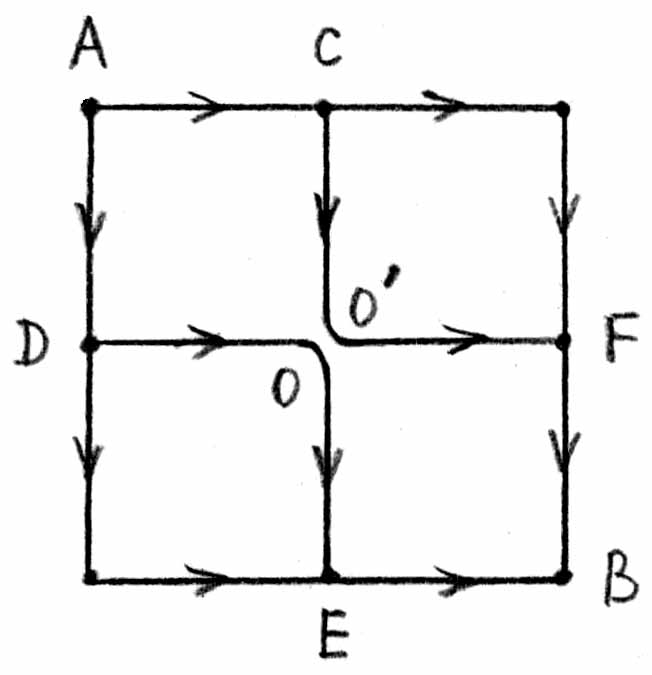
Из симметрии ясно, что токи через элементы CO и DO должны быть одинаковы и равны токам, текущим через элементы OF и OE. А раз так, то в точке О цепь можно разорвать, при этом токи через элементы сетки не изменятся:

 Рис.4.

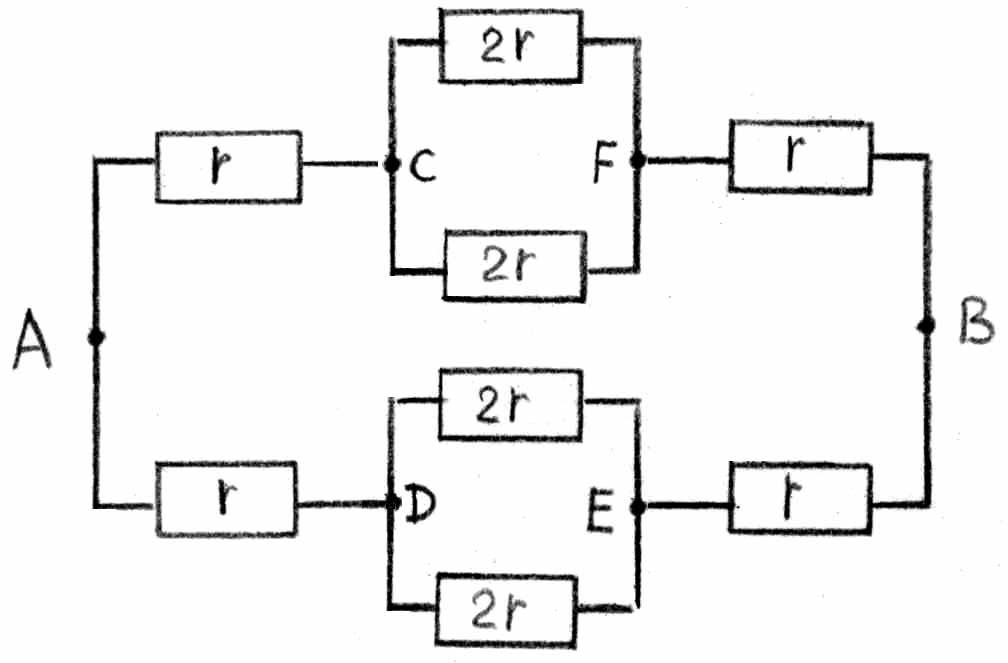
Последнюю схему уже можно представить в виде блоков последовательно и параллельно соединенных сопротивлений:

и определить полное сопротивление R_AB цепи:

2. Порядок выполнения работы.

2.1. Соберите на монтажном столе схему, показанную на рис. 3. Предусмотрите выключатель, соединяющий точки О и О^'. Выберите значения сопротивлений одинаковыми и равными 1 кОм.

2.2. Измерьте с помощью омметра сопротивление между точками А и В при замкнутом и разомкнутом положении выключателя. Объясните результаты измерений.

2.3. Подключите батарейку с ЭДС 1.5 вольта и последовательно с ней амперметр между точками А и В собранной Вами схемы. Измерьте силу тока при разомкнутом и замкнутом ключе. Измерьте напряжение между точками О и О^' при разомкнутом ключе и подключенной батарейке к точкам А и В.

Точки схемы, напряжение между которыми равно нулю, можно соединять и такое соединение не изменит токов, текущих по элементам схемы. Иногда такое соединение может существенно упростить схему.

3. Контрольные вопросы.

3.1. Какие свойства схемы могут оказаться полезными при расчете сложных схем?

3.2. Между какими точками схемы, изображенной на рис.3, напряжение равно нулю?

3.3. Исследуйте аналогичным способом сопротивление между противоположными вершинами проволочного куба? Чему равно сопротивление между этими точками?

Возврат в оглавление